 |
目次 前のページ |
−なぜ、あんな形をしているのか？−
なぜ“く"の字型や、手裏剣型になっていると安定して回転するのに、右のような普通の直線的なブーメランでは回転が不安定ですぐ止まってしまうのでしょうか。
下の図のような物体が回転する場合その回転軸は色々と考えられます。ところが、そのすべてが安定して回るわけではありません。
物体の回転を考える場合、慣性モーメント(慣性能率)という物を考えます。このモーメントとは、直線運動の慣性と同じく、回転体における慣性と思ってください。数学で定積分を学んだときに、簡単な物体ならそれを使って簡単に計算することができます。（参考までに慣性モーメントの式をのせておきます。）
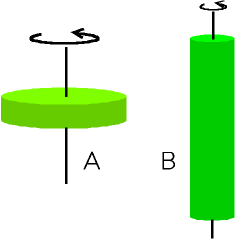
この慣性モーメントは感覚的に理解することも容易です。同じ質量の二つの物体を回す場合、Ｂの方がＡよりも回しやすい事が想像できます。角運度量は(慣性モーメント)×(角速度)ですから、同じ回転数で回転している時は、角運度量はＡの方がＢより大きく、同じ角運動量の場合はＡよりもＢの方が回転数が速くなります。
これは、フィギュアスケートで、手を頭上に伸ばすと回転数が早くなる事で皆さんも良くご覧になる現象です。
 |
さて、物体が２つ以上の回転軸を持つ場合、安定する回転軸は、慣性モーメントが最大の物と、最小の物のいずれかの場合で、その中間の物は不安定になります。
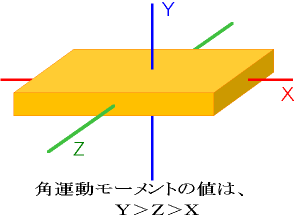
中間の物は、わずかでもフラツキがあると急激にフラツキが増大して回転が停止するか、安定した軸での回転に移行します。さきほどの長方形の板の場合は、最大の慣性モーメントと次の慣性モーメントの値が近く不安定になります。
《実験２》
空気抵抗を減らすため、針金で右のような形を作り、空中に放り上げて回転させてみましょう。一番安定して回るのはどれを軸にした場合でしょうか？
直線型でも、まったく回らなくはありません。
足なし竹トンボは、まさにこの形をしています。ただし、この竹トンボはブーメランと異なり回転面に平行に投げないためふらつきが少ないのと、非常に精巧に造られています。話はちょっとそれますが、足つきの竹トンボは最小慣性モーメントを持つ軸のまわりで回転しています。この足は、重心を下げるためではありません。その証拠に逆さにしても飛行します。また、足の長さが不十分だと《足中心の慣性モーメントが中位となり》、まったく飛行できません。竹トンボは精巧にできた足なし(またはごく短い)か、足が十分長い物のいずれかでないと飛びません。
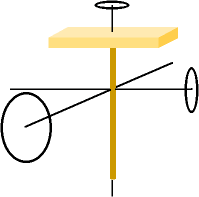 円の大きさは回転軸回りのモーメントの大きさを示す。  |
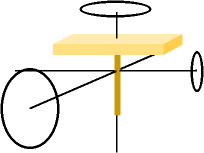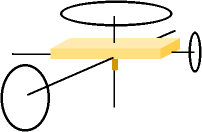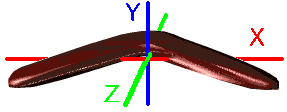
ブーメランは最大の慣性モーメントの軸(Ｙ軸)を中心に安定して回転し、２番目の値を持つ回転軸(Ｚ軸)と差があるため安定して飛行できます。もちろん２番目の物は空気抵抗の影響も大きいため、それも影響して安定して回ることはできません。
最小の慣性モーメントを持つ軸(Ｘ軸)では抵抗のない真空中では安定して回転できるはずです。
|
目次 前のページ |
